Chapitre 4 - Probabilités et conditionnement

Construire un arbre pondéré en lien avec une situation réelle
Déterminer des probabilités à l'aide d'un arbre pondéré
Calculer la probabilité d'un évènement connaissant ses probabilités conditionnelles par rapport à une partition de son univers

IRappels

1Définitions

On considère lors d'une expérience aléatoire, deux évènements $A$ et $B$ :

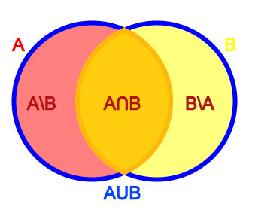
On appelle les évènements élémentaires les évènement constitués d'un seul élément
On appelle l'univers noté $\Omega$, l'ensemble de tous les évènements élémentaires
On note $\bar{A}$ l'évènement contraire à $A$
L'évènement "$A$ et $B$", noté $A \cap B$, est constitué des évènements élémentaires à la fois dans $A$ et dans $B$ (autrement dit, l'intersection des deux)
L'évènement "$A$ ou $B$", noté $A \cup B$, est constitué des évènements élémentaires se trouvant dans $A$ ou dans $B$ (autrement dit, la réunion des deux)
$\emptyset$ est l'évènement impossible
Si $A \cap B = \emptyset$, les deux évènements sont disjoints (ou incompatibles), et ne peuvent se produire en même temps
La probabilité de $A$ est la proportion du nombre d'éléments de A sur le nombre d'éléments total : $$ p (A) = \frac{Card (A)}{Card (\Omega)} $$

On considère l'expérience aléatoire "tirer un dé à 6 faces" et les deux évènements suivants :
$A$ : "Obtenir un nombre pair"
$B$ : "Obtenir un multiple de 3"

Il y a 6 évènements élémentaires : "Obtenir 1", "Obtenir 2", etc. On les note $\{1\}, \{2\}, \{3\}, \{4\}, \{5\}$ et $\{6\}$.
L'univers $\Omega$contient tous les évènements élémentaires (toutes les possibilités) : $\Omega = \{1,2,3,4,5,6\}$
L'évènement $A$ contient tous les évènements élémentaires correspondant à un nombre pair : $A = \{2,4,6\}$, et \{B=\{3,6\}\}
L'évènemente \{\bar{A}\} est l'évènement "Obtenir un nombre impair" : $\bar{A} = \{1,3,5\}$
L'évènemente \{A \cap B\} est l'évènement "Obtenir un nombre pair et multiple de 3" : $A\cap B = \{6\}$ (autrement dit, "Obtenir 6")
L'évènemente \{A \cup B\} est l'évènement "Obtenir un nombre pair ou multiple de 3" : $A\cup B = \{2,3,4,6\}$
L'évènement "Obtenir un nombre pair et multiple de 5" est impossible, il s'agit de l'évènement $\emptyset$
On calcule la probabilité des évènements $A$ et $B$ : $$ p (A) = \frac{Card (\{2,4,6\})}{Card (\{1,2,3,4,5,6\})} = \frac{3}{6} = \frac{1}{2}=0,5 \\ p (B) = \frac{Card (\{3,6\})}{Card (\{1,2,3,4,5,6\})} = \frac{2}{6} = \frac{1}{3} \simeq 0,33 \\ $$

2Arbre pondéré

Les arbres mathématiques sont souvent utilisés pour représenter des scénarios à choix avec différentes issues possibles. Ils sont donc utilisés en probabilité lorsque l'on étudie plusieurs évènements.

Représentons à l'aide d'un arbre, une expérience aléatoire sur un lycée de 1000 élèves où nous tirons au hasard la fiche de renseignement d'un élève :

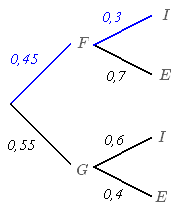
L'univers $\Omega$est l'ensemble des élèves
L'évènement $G$ est "l'élèvé est un garçon", l'évènement contraire $\bar{G}$, noté $F$ est "l'élève est une fille"
L'évènement $E$ est "l'élèvé est externe", l'évènement contraire $\bar{E}$, noté $I$ est "l'élève est interne"

Nous savons qu'il y a 45% de filles et 55% de garçons dans ce lycée. Parmi les filles 30% sont internes et 70% externes. Parmi les garçons, 60% sont internes et 40% externes.
La situation se représente par un arbre pondéré :

Deux propriétés se vérifient sur un arbre pondéré :

La somme des probabilités de branches issues d'un même noeud, vaut 1
La probabilité d'un évènement correspondant à un chemin vaut le produit des probabilités de chaque branche du chemin

Sur notre exemple, on constate effectivement que :

$p (F) + p (G) = 1$
Le chemin bleu correspond à l\évènement "l'élève est une fille interne", correspondant à 30% de 45% des élèves, donc $\frac{30}{100} \times \frac{45}{100} \times 100= 13,5%$ des élèves. On retrouve ce résultat en multipliant les probabilités des deux branches : $0,45 \times 0,3 = 0,135$.

IINotion de probabilité conditionnelle

Dans cette partie, on note $A$ et $B$ deux évènements d'une expérience aléatoire.

On note $p_A (B)$ la probabilité de $B$ sachant que A s'est déjà produit.

Sur un arbre pondéré, on représente les évènements possibles avec $A$ antérieur à $B$. Les probabilités conditionnelles se lisent sur les deuxièmes branches en partant du premier noeud :

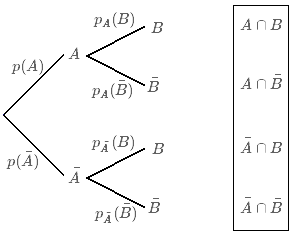
En reprenant l'exemple du I.2., on peut lire les probabilités conditionnelles :

La probabilité de choisir un élève interne parmi les filles est p_F (I)=0,3
La probabilité de choisir un élève externe parmi les filles p_F (E)=0,7
la probabilité de choisir un élève interne parmi les garçons p_G (I)=0,6
la probabilité de choisir un élève externe parmi les garçons p_G (E)=0,4

En reprenant la propriété de multiplication des probabilités dans le I.2. , on obtient la formule suivante :

$p (A \cap B) = p (A) p_A (B)$

Il est donc possible de calculer la probabilité conditionnelle par la formule déduite :

$p_A (B) = \frac{p (A \cap B)}{p (A)}$

IIIPartition d'un univers et formule des probabilités totales